Python-Problems

Daily Python Problems

Weekly issues(start:2021/4/16)

Special Edition: Recursion7

Q7Levenshtein

在计算文本的相似性时，经常会用到编辑距离。编辑距离，又称Levenshtein距离，是指两个字串之间，由一个转成另一个所需的最少编辑操作次数。通常来说，编辑距离越小，两个文本的相似性越大。这里的编辑操作主要包括三种：

  • 插入：将一个字符插入某个字符串；
  • 删除：将字符串中的某个字符删除；
  • 替换：将字符串中的某个字符替换为另外一个字符。

当两个字符串都为空串，那么编辑距离为0；

当其中一个字符串为空串时，那么编辑距离为另一个非空字符串的长度；

当两个字符串均为非空时(长度分别为 i 和 j )，取以下三种情况最小值即可：

  • 长度分别为 i-1 和 j 的字符串的编辑距离已知，那么加1即可；
  • 长度分别为 i 和 j-1 的字符串的编辑距离已知，那么加1即可；
  • 长度分别为 i-1 和 j-1 的字符串的编辑距离已知，此时考虑两种情况，若第i个字符和第j个字符不同，那么加1即可；如果不同，那么不需要加1。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
def minDistance(word1, word2):
    if not word1:
        return len(word2 or '') or 0

    if not word2:
        return len(word1 or '') or 0

    size1 = len(word1)
    size2 = len(word2)

    last = 0
    tmp = range(size2 + 1)
    value = None

    for i in range(size1):
        tmp[0] = i + 1
        last = i
        # print word1[i], last, tmp
        for j in range(size2):
            if word1[i] == word2[j]:
                value = last
            else:
                value = 1 + min(last, tmp[j], tmp[j + 1])
                # print(last, tmp[j], tmp[j + 1], value)
            last = tmp[j+1]
            tmp[j+1] = value
        # print tmp
    return value

==optimization==>

def editdistance(str1, str2):

    edit = [[i + j for j in range(len(str2) + 1)] for i in range(len(str1) + 1)]

    for i in range(1, len(str1) + 1):
        for j in range(1, len(str2) + 1):

            if str1[i - 1] == str2[j - 1]:
                d = 0
            else:
                d = 1

            edit[i][j] = min(edit[i - 1][j] + 1, edit[i][j - 1] + 1, edit[i - 1][j - 1] + d)

    return edit[len(str1)][len(str2)]


print(editdistance('hello', 'he'))
>>
3

Q6Pascal Triangle

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# Function Method
def triangle():
    N = [1]
    while True:
        yield N     # generator特点在于：在执行过程中，遇到yield就中断，下次又继续执行
        N.append(0)  # 每次都要在最后一位加个0，用于后续的叠加
        N = [N[i]+N[i-1] for i in range(len(N))]
 
def print_triangle(x):
    a = 0
    for t in triangle():  # 这里可以每次调用一个N（得力于Yield函数）
        print(t)
        a += 1
        if a ==x:
             break
print_triangle(10) # 打印10行

# ----------------------------------------

N = [1]
for i in range(10):  # 打印10行
    print(N)
    N.append(0)
    N = [N[k] + N[k-1] for k in range(i+2)]
    
==optimization==>

N = [1]  # 先把第一行给定义好
for i in range(10):  # 打印10行
    # 从这里开始我们就要把list转换为一个居中的字符串打印出来
    L = N.copy()   # 我们需要吧N复制给L,而不能直接L = N，因为这样L和N会在同一个地址，后续算法就会出错
    for j in range(len(L)):   # 遍历和转化
        temp = str(L[j])
        L[j] = temp
    l = ' '.join(L).center(50)  # 组合和剧中一起写
    print(l)      # 这里就是打印l了
    N.append(0)   # 因为复制之后L是L，N是N，所以我们还是继续在N末尾加0
    N = [N[k] + N[k-1] for k in range(i+2)]

Q5River Crossing Problem【Unsolved】

写一个程序来解决这样一个问题:3只羚羊和3只狮子准备乘船过河，河边有一艘能容纳2只动物的小船。但是,如果两侧河岸上的狮子数量大于羚羊数量,羚羊就会被吃掉。找到运送办法，使得所有动物都能安全渡河。

1

Q4Least Common Multiple

1
2
3
4
5
6
7
8
9
10
11
def lcm(a, b):
    c = a
    while True:
        if c % a == 0 and c % b == 0:
            print(c)
            break
        c += 1

lcm(8, 2)
>>
8

Q3Gread Common Divisor

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# recursion method
def gcd(self, x, y):
    if y == 0:
        return x
    else:
        return self.gcd(y, x % y)
==optimization==>>   
def gcd(a, b):
	if b == 0:return a
	return gcd(b, a % b)

# Euclid Algorithm(Toss and divide)
def gcd(m,n):
    """Euclid Algorithm:calculate the greatest common divisor"""
    while m % n != 0:
        oldm = m
        oldn = n
        
        m = oldn
        n = oldm % oldn
    return n
==optimization==>>
def gcd(m, n):
    """Euclid Algorithm:calculate the greatest common divisor"""
    while m % n != 0:
        m, n = n, m % n
    return n

Q2Three Water Problem

====essential===> target_number % gcd == 0

贝祖定理/裴蜀定理：对任何整数a、b和它们的最大公约数d，关于未知数x和y的线性不定方程（称为裴蜀等式）：若a,b是整数,且gcd(a,b)=d，那么对于任意的整数x,y–>ax+by都一定是d的倍数，特别地，一定存在整数x,y，使ax+by=d成立。

倒水问题属于数论应用题，可以运用丢番图方程进行解答。丢番图方程 ax+by=c (a、b、c是整数)有解，当且仅当c||gcd(a,b)成立

<<整数a、b和它们的最大公约数c。

一定存在整数x,y，使ax+by=c成立。

若d是c的倍数，显然也一定存在整数x,y，使得 ax+by=d成立。>>

实际上，两个容量互质的水杯，可以倒出任意容量的水。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution:
    def canMeasureWater(self, x, y, z):
        """
        :type x: int
        :type y: int
        :type z: int
        :rtype: bool
        """
        tmp = self.gcd(x, y)
        if z == 0:
            return True
        if z > x + y:
            return False
        else:
            return z % tmp == 0

    def gcd(self, x, y):
        if y == 0:
            return x
        else:
            return self.gcd(y, x % y)

ans = Solution()
b = ans.canMeasureWater(5, 3, 4)
print(b)
>>
True

use recursion to calculate the sum of list

Q1Sum List

1
2
3
4
5
6
7
8
9
10
11
12
13
# common case
def sum(alist):
    ans = 0
    for x in alist:
        ans += x
    return ans

# recursive case
def sum(alist):
    if len(alist) == 1:
		return alist[0]
    else:
        return alist[0] + sum(alist[1:])

FirthIssue(5/22-27)4

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
# Method one
def binary_search(alist, item):
    found = False
    while not found:
        n = len(alist) % 2

        if n != 0:
            base_num = (len(alist) + 1) // 2
        else:
            base_num = len(alist) // 2

        if len(alist) == 1:
            base_num = 0

        if alist[base_num] == item:
            found = True
        elif alist[base_num] > item:
            alist = alist[:base_num]
            print(alist)
        elif alist[base_num] < item:
            alist = alist[base_num:]
            print(alist)

    return found
# Merhod Two[the best way]
def binary_search(alist, item):
    first = 0
    last = len(alist) - 1
    found = False
    
    while first <= last and not found:
        midpoint = (first + last) // 2
        if alist[midpoint] == item:
            found = True
        else:
            if item < alist[midpoint]:
                last = midpoint - 1
            else:
                first = midpoint + 1
	return found


# Method three: Recuesion
def binary_search_recursion(alist, item):
    if len(alist) == 0:
        return False
    else:
        midpos = len(alist) // 2
        if alist[midpos] == item:
            return True
        else:
            if item < alist[midpos]:
                return binary_search_recursion(alist[:midpos], item)
            else:
                return binary_search_recursion(alist[midpos+1:], item)

lst = [1, 2, 3, 4, 5, 6, 7, 8, 9]
print(binary_search(lst, 5))
>>
[1, 2, 3, 4, 5]
[4, 5]
True
>>test 100 tiems
method 1: 0.0007410999999999945
method 2: 3.929999999999212e-05
method 3(recursion): 1.1018111

Q3Fibonacci Sequence

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#---- Recursion[the worst way*] ----
def Fibonacci_Recursion_tool(n):
    if n <= 0:
        return 0
    elif n == 1:
        return 1
    else:
        return Fibonacci_Recursion_tool(n - 1) + Fibonacci_Recursion_tool(n - 2)


def Fibonacci_Recursion(n):
    result_list = []
    for i in range(1, n + 1):
        result_list.append(Fibonacci_Recursion_tool(i))
    return result_list

#---- Loop [the best way****] ----
def Fibonacci_Loop_tool(n):
    a, b = 0, 1
    while n > 0:
        a, b = b, a + b
        n -= 1


def Fibonacci_Loop(n):
    result_list = []
    a, b = 0, 1
    while n > 0:
        result_list.append(b)
        a, b = b, a + b
        n -= 1
    return result_list

#---- Yield [the best way****] ----
def Fibonacci_Yield_tool(n):
    a, b = 0, 1
    while n > 0:
        yield b
        a, b = b, a + b
        n -= 1


def Fibonacci_Yield(n):
    # return [f for i, f in enumerate(Fibonacci_Yield_tool(n))]
    return list(Fibonacci_Yield_tool(n))

>>
print(Fibonacci_Recursion(5))
[1, 1, 2, 3, 5]

Q2Recursion List

1
2
3
4
5
6
7
8
9
10
11
def rev_list(l):
    if len(l) == 1:
        return l
    else:
        return [l[-1]] + rev_list(l[:-1])  # -1 才算是取最后一位之前的所有

lst = [1, 2, 3, 4, 5]
b = rev_list(lst)
print(b)
>>
[5, 4, 3, 2, 1]

Q1Greedy Algorithm

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
def dpmakechange(coinvaluelist, change, mincoins, coinsused):
    for cents in range(change+1):
        coincount = cents
        newcoin = 1
        for j in [c for c in coinvaluelist if c <= cents]:
            if mincoins[cents-j] + 1 < coincount:
                coincount = mincoins[cents - j] + 1
                newcoin = j
        mincoins[cents] = coincount
        coinsused[cents] = newcoin
    return mincoins

def printcoins(coinsused, change):
    coin = change
    while coin > 0:
        thiscoin = coinsused[coin]
        print(thiscoin)
        coin -= thiscoin

c1 = [1, 5, 10, 21, 25]
coinsused = [0] * 64
coincount = [0] * 64
dpmakechange(c1, 63, coincount, coinsused)
printcoins(coinsused, 63)
print('--------')
printcoins(coinsused, 52)
print('--------')
print(coinsused)

>>
21
21
21
--------
10
21
21
--------
[1, 1, 1, 1, 1, 5, 1, 1, 1, 1, 10, 1, 1, 1, 1, 5, 1, 1, 1, 1, 10, 21, 1, 1, 1, 25, 1, 1, 1, 1, 5, 10, 1, 1, 1, 10, 1, 1, 1, 1, 5, 10, 21, 1, 1, 10, 21, 1, 1, 1, 25, 1, 10, 1, 1, 5, 10, 1, 1, 1, 10, 1, 10, 21]

FourthIssue(5/14-22)6

Q6Tower of Hanoi

1
2
3
4
5
6
7
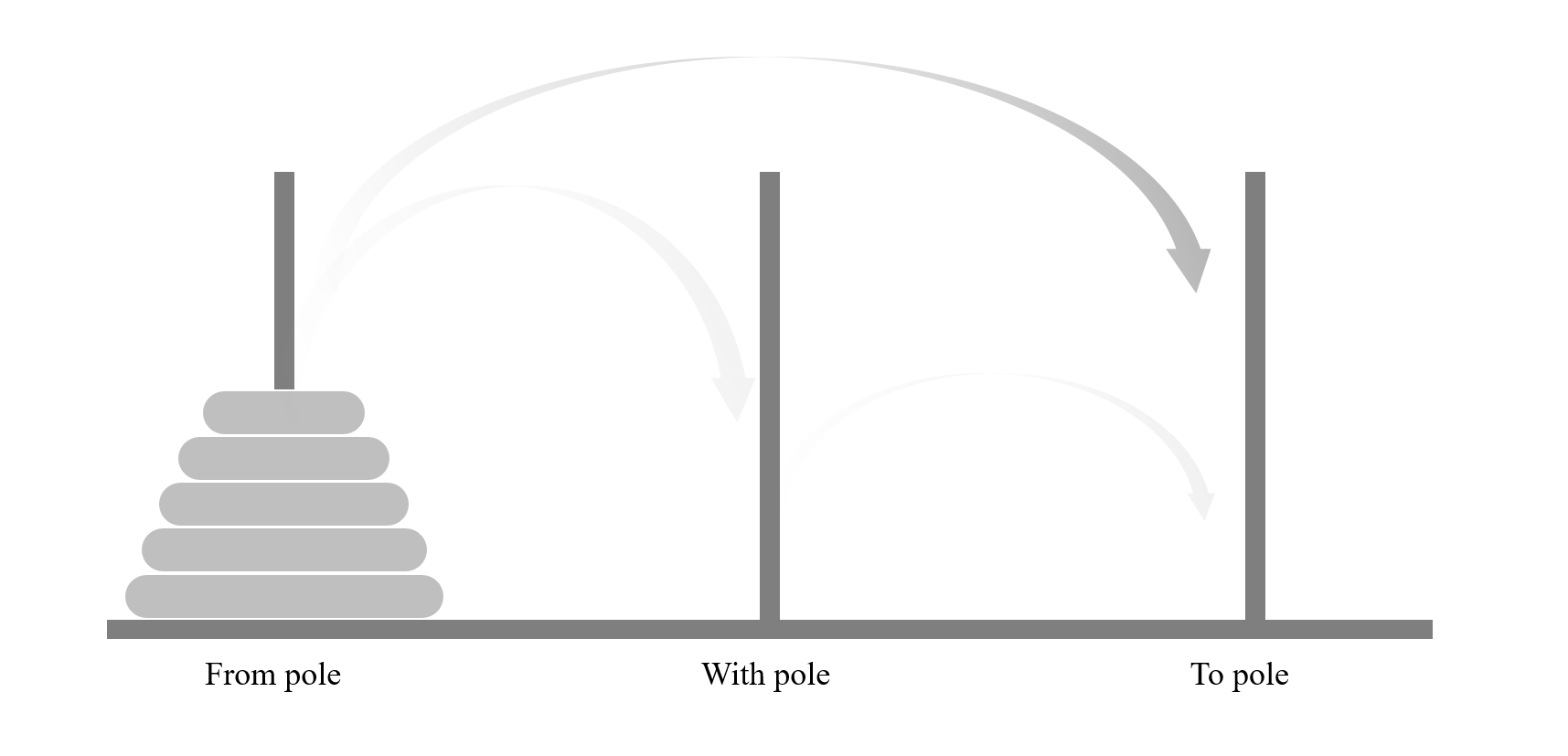
8
def movedisk(fp, tp):
    print('moving disk from %d to %d' % (fp, ))

def movetower(height, frompole, topole, withpole):
    if height > 1:
        movetower(height-1, frompole, withpole, topole)
        movedisk(frompole, topole)
        movetower(height-1, withpole, topole, frompole)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def hanoi(n, x, y, z):
    global count
    if n == 1:
        print('第%d步：从%s到%s' % (count, x, z))
        count += 1
    else:
        hanoi(n - 1, x, z, y)  # 将n-1个盘子由X移动到Y上
        print('第%d步：从%s到%s' % (count, x, z))  # 将最底下的盘子由X移动到Z上。
        count += 1
        hanoi(n - 1, y, x, z)  # 将Y上的n-1个盘子由Y移动到Z上

count = 1
n = 3
hanoi(n, 'X', 'Y', 'Z')
>>
第1步：从X到Z
第2步：从X到Y
第3步：从Z到Y
第4步：从X到Z
第5步：从Y到X
第6步：从Y到Z
第7步：从X到Z

Q5Integer to arbitary base string

key steps: tostr(n//base, base)

1
2
3
4
5
6
7
8
9
10
# uesing recursion
def tostr(n, base):
    convertstring = '0123456789ABCDEF'
    if n < base:
        return convertstring[n]
    else:
        return tostr(n//base, base) + convertstring[n % base]
tostr(8, 2)
>>
1000
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# useing stack 
def tostr(n, base):
    templist = []
    convertstring = '0123456789ABCDEF'
    if n < base:
        templist.insert(0, convertstring[n])
    else:
        templist.insert(0, convertstring[n % base])
        tostr(n//base, base)
    return ''.join(temlist)

tostr(8, 2)
>>
1000

Q4InfixExp convert PostExp

Q3Unordered Linked List

implement unordered linked list by python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
class Node:

    def __init__(self, initdata):
        self.data = initdata
        self.next = None

    def getData(self):
        return self.data

    def getNext(self):
        return self.next

    def setData(self, item):
        self.data = item

    def setNext(self, newnext):
        self.next = newnext

    def __repr__(self):
        return '%s--%s' % (self.data, self.next)


class Unorderlist:
    def __init__(self):
        self.head = None

    def isEmpty(self):
        return self.head is None

    def length(self):
        current = self.head
        count = 0
        while current is not None:
            current = current.getNext()
            count += 1

        return count

    def add(self, item):
        temp = Node(item)
        temp.setNext(self.head)
        self.head = temp

    def search(self, item):
        current = self.head
        found = False
        while current is not None and not found:
            if current.getData() == item:
                found = True
            else:
                current = current.getNext()
        return found

    def remove(self, item):
        current = self.head
        previous = None
        found = False
        while not found:
            if current.getData() == item:
                found = True
            else:
                previous = current
                current = current.getNext()
        if previous is None:
            self.head = current.getNext()
        else:
            previous.setNext(current.getNext())

    def __repr__(self):
        return 'the linked list is %s' % self.head

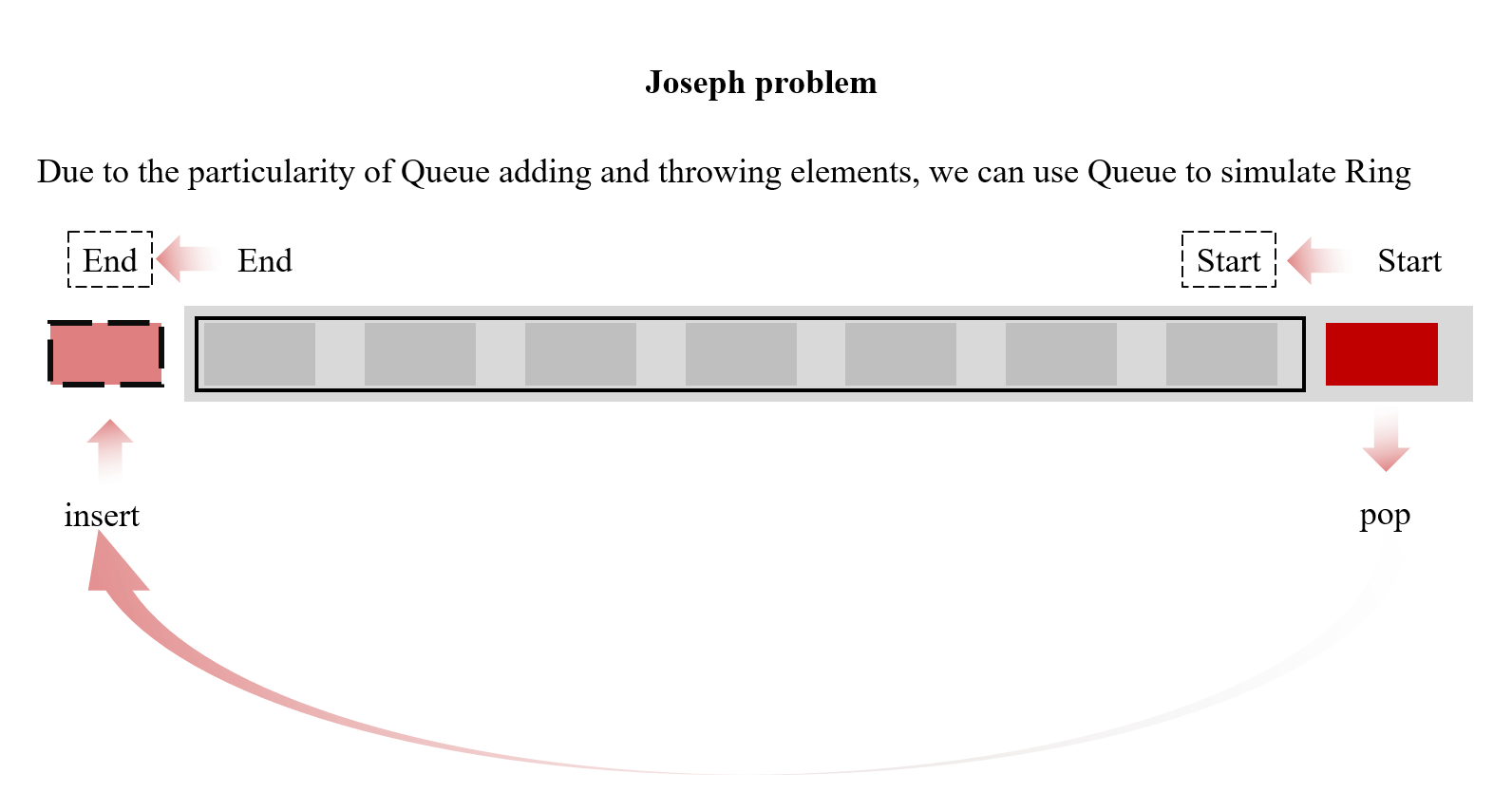
Q2Joseph ring problem

we can simulate a ring with Queue, the essential of joseph ring problem is Queue Problem

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
print(listname)

def simulation_pass_potatoes(listname, num):

    while len(listname) != 1:
        for i in range(num):
            cur_ele = listname.pop()
            listname.insert(0, cur_ele)
        listname.pop()
        print(listname)
    print(listname)

simulation_pass_potatoes(listname, 7)
>>
['brad', 'kent', 'jane', 'susan', 'david', 'bill']
['bill', 'brad', 'kent', 'jane', 'susan']
['jane', 'susan', 'bill', 'brad']
['susan', 'bill', 'brad']
['brad', 'susan']
['susan']

Q1Fixed-Point Problem

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
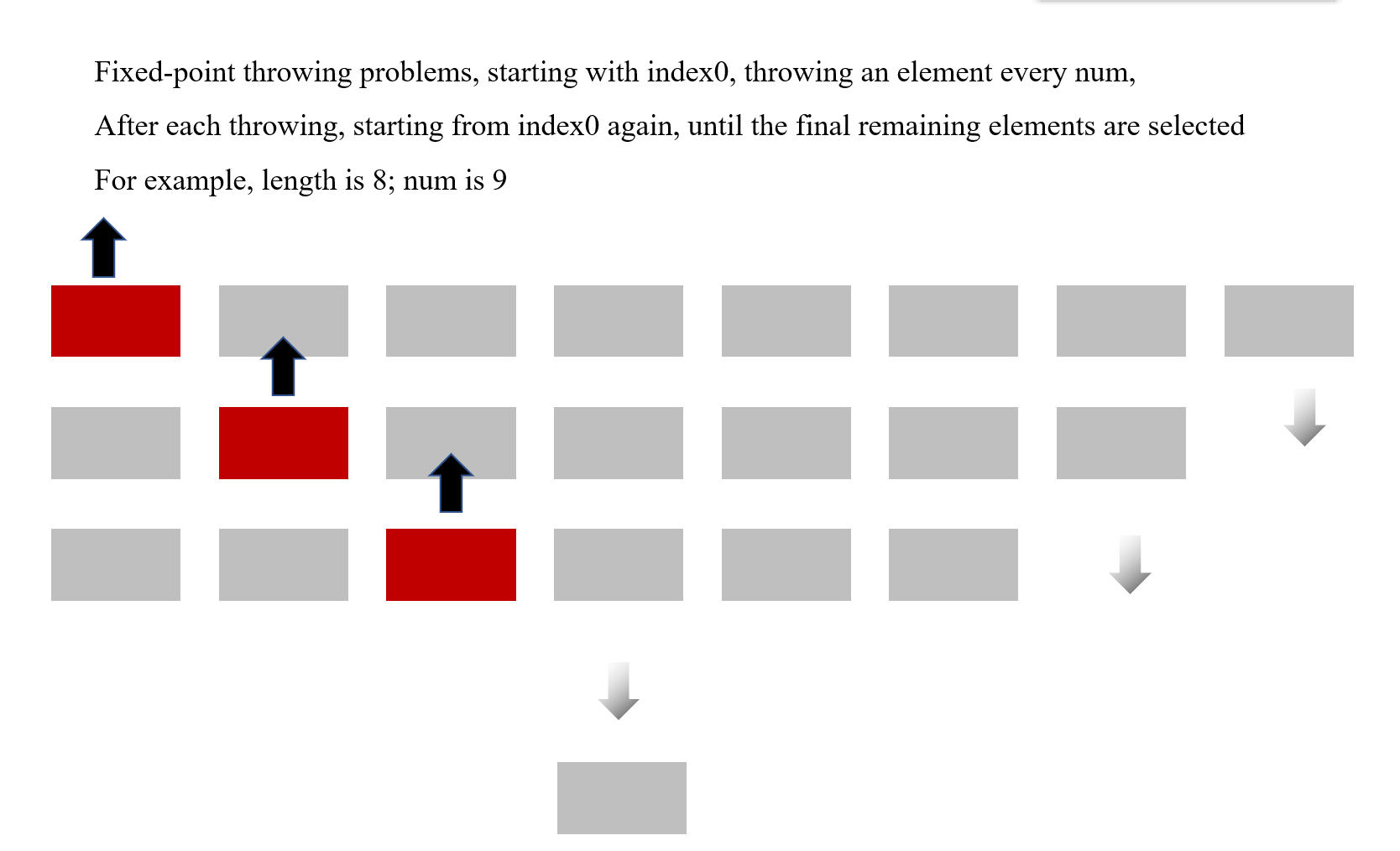
27
def post_potatoes(namelist, num):
    cur_list = namelist.copy()
    print(cur_list)

    while len(cur_list) != 1:
        if len(cur_list) >= num:
            index = num - 1
            cur_list.pop(index)
            print(cur_list)
        else:
            index = num % len(cur_list) - 1
            cur_list.pop(index)
            print(cur_list)
    print(cur_list)
    return cur_list

name_list = ['drink', 'star', 'fire', 'drinking', 'drinkle', 'top']
num = 4

post_potatoes(name_list, num)
>>
['drink', 'star', 'fire', 'drinking', 'drinkle', 'top']
['drink', 'star', 'fire', 'drinkle', 'top']
['drink', 'star', 'fire', 'top']
['drink', 'star', 'fire']
['star', 'fire']
['star']

ThirdIssue(5/10-14)4

Q4:Convert list to String

use the builtin function:''.join(list)

1
2
3
4
5
6
7
temp_list = [chr(i) for i in range(65, 91)]
str = ''.join(temp_list)
str1 = '.'.join(temp_list)
print(str)
>>ABCDEFGHIJKLMNOPQRSTUVWXYZ
print(str1)
>>A.B.C.D.E.F.G.H.I.J.K.L.M.N.O.P.Q.R.S.T.U.V.W.X.Y.Z

Q3:Pre/Middle/PostExpression Conversion

Middle Expression Per Expression Post Expression
A + B + A B A B +
A + (B * C) + A * B C A B C * +
(A + B) * C *+ A B A B + C *

The preorder expression requires all operators to appear before the two operands it acts on ps: pay attention to bracket

First in First out

InfixExp(中序表达式)转换PostfixExp(后序表达式)算法：

1）当输入的是操作数时候，直接输出到后序表达式PostfixExp序列中

2）当输入开括号时候，把它压栈

3）当输入的是闭括号时候，先判断栈是否为空，若为空，则发生错误并进行相关处理。若非空，把栈中元素依次弹出并输出到Postfix中，知道遇到第一个开括号，若没有遇到开括号，也发生错误，进行相关处理

4）当输入是运算符op（+、- 、×、/）时候

a)循环，当（栈非空and栈顶不是开括号and栈顶运算符的优先级不低于输入的运算符的优先级）时，反复操作：将栈顶元素弹出并添加到Postfix中

b)把输入的运算符op压栈

5）当中序表达式InfixExp的符号序列全部读入后，若栈内扔有元素，把他们依次弹出并放到后序表达式PostfixExp序列尾部。若弹出的元素遇到空括号，则说明不匹配，发生错误，并进行相关处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# convert middle-expression to post expression
def infixToPostfix(infixerpr):
    temp_list = [chr(i) for i in range(65, 91)]
    alphabet = ''.join(temp_list)
    priority_dict = {'*': 3, '/': 3, '+': 2, '-': 2, '(': 1}

    Operators = []
    AlphaBet = []

    input_str_to_list = infixerpr.split()

    for element in input_str_to_list:
        if element in alphabet:
            AlphaBet.append(element)
        elif element == '(':
            Operators.append(element)
        elif element == ')':
            tempelement = Operators.pop()
            while tempelement != '(':
                AlphaBet.append(tempelement)
                tempelement = Operators.pop()
        else:
            while (len(Operators) != 0) and (priority_dict[Operators[len(Operators)-1]] >= priority_dict[element]):
                AlphaBet.append(Operators.pop())
            Operators.append(element)

    while len(Operators) != 0:
        AlphaBet.append(Operators.pop())
    print(" ".join(AlphaBet))


infixToPostfix('( A + B ) * ( C + D )')
infixToPostfix('( A + B )')
>> A B + C D + *
>> A B +

Q2.1Calculate Post Expression

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def post_calculateion_expression(postfixexpr):
    list1 = []

    tokenlist = postfixexpr.split()

    for token in tokenlist:
        if token in '0123456789':
            list1.append(int(token))
        else:
            operand2 = list1.pop()
            operand1 = list1.pop()
            result = doMath(token, operand1, operand2)
            list1.append(result)
    return list1.pop()


def doMath(op, op1, op2):
    if op == '*':
        return op1 * op2
    elif op == '/':
        return op1 / op2
    elif op == '+':
        return op1 + op2
    else:
        return op1 - op2


a = post_calculateion_expression('1 2 + 3 *')
print(a)
>>9

Q1:BaseConversion

Decimal Conversion

remainder number optimization by string`s index

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
def decimal(num):

    bin_num = []

    while num > 0:
        rem = num % 12
        num //= 12
        if rem in [10, 11, 12]:
            if rem == 10:
                bin_num.append('A')
            elif rem == 11:
                bin_num.append('B')
            elif rem == 12:
                bin_num.append('C')
        else:
            bin_num.append(rem)

    bin_num.reverse()

    ans = ''
    for x in bin_num:
        ans = ans + str(x)
    print(ans)
# remaind number`s optimization, Take hexadecimal as an example

def decimal_conversion(num):
    
    digits = '0123456789ABCDEF'
    
    con_num = []
    
    while num > 0:
        rem = num % 16
        num //= 16
        con_num.append(digits[rem])
    
    con_num.reserve()
    
    ans = ''
    for x in con_num:
        ans = ans + str(x)
    print(ans)

Second Issue(5/3-8)3

Q3:RegularExpression

https://deerchao.cn/tutorials/regex/regex.htm

注意：本题是整个面试流程中的第一道开卷试题。
请写一个 匹配 简历中 中英文本科学位名称 的 Python 正则表达式。
本题考察的技能和思维严谨性是这份工作最需要的，请仔细查一查想一想，最好上机调试一下，再作答。

简历中 描述本科学位，一般说：“Bachelor”, “本科”，等等。举几个从实际简历pdf提取的文字例子：
例1：
Education
Philippines University MBA
Pepperdine University – Malibu, CA Bachelor of Arts, Economics
要求正则匹配“Bachelor”。
例2：
学历教育
中国地质大学（武汉）地理信息系统专业——硕士
中国地质大学（武汉）地理信息系统专业——工学学士
要求正则匹配“学士”。
例3：
EDUCATION
Bachelor of Science in CSE/Bio-engineering; Bioinformatics, University of California, San Diego.
要求正则匹配“Bachelor”。

1
2
3
4
5
6
7
8
9
10
11
import re

text1 = 'Pepperdine University – Malibu, CA Bachelor of Arts, Economics'
text2 = '中国地质大学（武汉）地理信息系统专业——工学学士'
text3 = 'Bachelor of Science in CSE/Bio-engineering; Bioinformatics, University of California, San Diego.'

pattern0 = r'\bBachelor.*|\B专业.*|\bBachelor.*\b'

ans = re.search(pattern0, text1)

print(ans.group())

Q2:Match Brackets

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import Stack

def match_brackets(str1):
    
    s = Stack()
    balanced = True
    index = 0
    while index < len(str1) and balanced:
        symbol = str1[index
        if symbol == '(':
            s.push(symbol)
        else:
            if s.isEmpty():
                balanced = False
            else: 
                s.pop()
        index += 1
    if balanced and s.isEmpty():
        retuen True
    else:

Q1:Heterologous Detection

Method1Counting

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def counting_method(s1, s2):
    c1 = [0] * 26
    c2 = [0] * 26

    for i in range(len(s1)):
        pos = ord(s1[i]) - ord('a')
        c1[pos] += 1

    for i in range(len(s2)):
        pos = ord(s2[i]) - ord('a')
        c2[pos] += 1

    j = 0
    stillok = True
    while j < 26 and stillok:
        if c1[j] == c2[j]:
            j += 1
        else:
            stillok = False

    return stillok

ord(character) –return–>the ascii code

example: ord(‘a’)–return–> 97

Method2Sorting

1
2
3
4
5
6
7
8
9
10
11
12
13
def sortingmethod(s1, s2):
	list1 = list(s1)
	list2 = list(s2)
	
    list1.sort()
    list2.sort()
    
	if list1 == list2:
		print(list1)
        return True
    else:
        print(list1 '\n' list2)
        return False

First Issue(4/16-4/23)2

Q2:Fraction Class

create a instance to inplement the fraction`s add-method

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def gcd(m, n):
    """Euclid Algorithm:calculate the greatest common divisor"""
    while m % n != 0:
        m, n = n, m % n
    return n

class Fraction():
    
    def __init__(self, top, bottom):
        self.top = top
        self.bottom = bottom
    
    def show(self):
        print(str(self.top) + '/' + str(self.bottom))
    
    def __add__(self, otherfraction)
    	newtop = self.top * otherfraction.bottom + \
        	self.bottom * otherfraction.top
        newbottom = self.bottom * otherfraction.bottom
        common = gcd(newtop, newbottom)
        return Fraction(newtop//common, newbottom//common)
    
    def __str__(self):
        return(str(self.top) + '/' + str(self.bottom))

f1 = Fraction(1, 5)
f2 = Fraction(2, 4)
f3 = f1 + f2 # __add__ ==> '+'
print(f3) # __str__ ==> return->str(Fraction)

Q1:Split string into individual letters

1
2
3
4
5
6
7
8
9
10
11
12
13
string = 'ab_cdefg'
y = []
alphabet = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h',
            'i', 'j', 'q', 'l', 'm', 'n', 'o', 'p',
            'q', 'r', 's', 't', 'u', 'v', 'w', 'x',
            'y', 'z']
# another method about calling alphabet
# alphabet = [chr(i) for i in range(97, 123)]
for i in string:
    print(i)
    if i in alphabet:
        y.append(i)
print(y)
  • number(0-9):the representation of ASCII is 48~57
  • Lower case letters(a-z):the representation of ASCII is 97~122
  • uppercase letters(A-Z):the representation of ASCII is 65~90

ASCII: American standard code for information interchange