Infectious Disease Model

概念介绍

S (Susceptible)易感者指缺乏免疫能力健康人，与感染者接触后容易受到感染；

E (Exposed)暴露者 指接触过感染者但暂无传染性的人，可用于存在潜伏期的传染病；

I (Infectious)患病者指有传染性的病人，可以传播给 S，将其变为 E 或 I ；

R (Recovered)康复者指病愈后具有免疫力的人，如是终身免疫性传染病，则不可被重新变为 S 、E 或 I ，如果免疫期有限，就可以重新变为 S 类，进而被感染。

各个变量之间并不是相互独立，而是可以相互转化。

The various variables are not independent of each other, but can be transformed into each other.

COVID19 3.7-3.8

模型一：SI-Model

不进行人为的控制

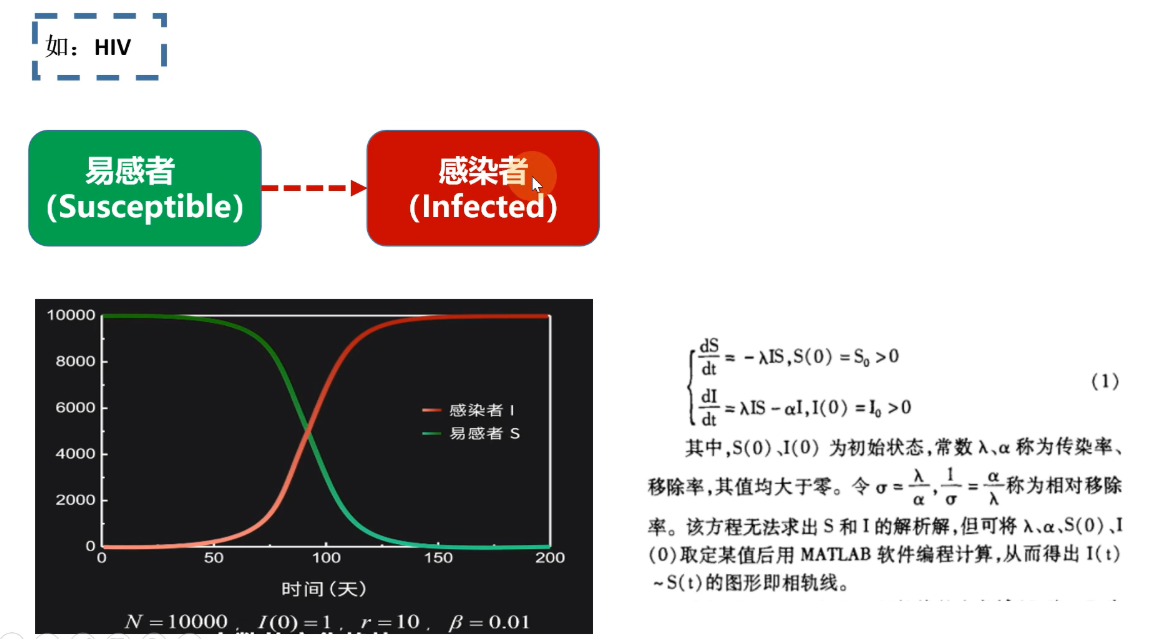
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
import scipy.integrate as spi
import numpy as np
import matplotlib.pyplot as plt

# N为人群总数
N = 10000
# β为传染率系数
beta = 0.25
# gamma为恢复率系数
gamma = 0
# I_0为感染者的初始人数
I_0 = 1
# S_0为易感者的初始人数
S_0 = N - I_0
# T为传播时间
T = 150

# INI为初始状态下的数组
INI = (S_0,I_0)


def funcSI(inivalue,_):
    Y = np.zeros(2)
    X = inivalue
    # 易感个体变化
    Y[0] = - (beta * X[0] * X[1]) / N + gamma * X[1]
    # 感染个体变化
    Y[1] = (beta * X[0] * X[1]) / N - gamma * X[1]
    return Y

T_range = np.arange(0,T + 1)

RES = spi.odeint(funcSI,INI,T_range)

plt.plot(RES[:,0],color = 'darkblue',label = 'Susceptible',marker = '.')
plt.plot(RES[:,1],color = 'red',label = 'Infection',marker = '.')
plt.title('SI Model')
plt.legend()
plt.xlabel('Day')
plt.ylabel('Number')
plt.show()

模型二：SIS-Model

易感染者–>感染者—TIME—>易感染者

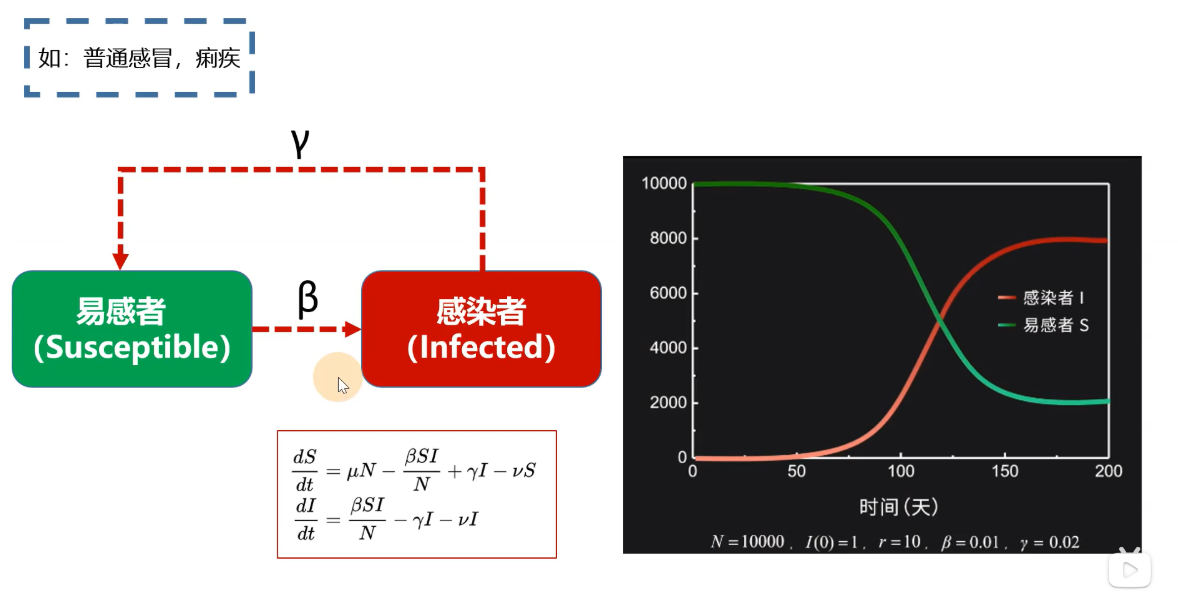
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
import scipy.integrate as spi
import numpy as np
import matplotlib.pyplot as plt

# N为人群总数
N = 10000
# β为传染率系数
beta = 0.25
# gamma为恢复率系数
gamma = 0.05
# I_0为感染者的初始人数
I_0 = 1
# S_0为易感者的初始人数
S_0 = N - I_0
# T为传播时间
T = 150

# INI为初始状态下的数组
INI = (S_0,I_0)


def funcSIS(inivalue,_):
    Y = np.zeros(2)
    X = inivalue
    # 易感个体变化
    Y[0] = - (beta * X[0]) / N * X[1] + gamma * X[1]
    # 感染个体变化
    Y[1] = (beta * X[0] * X[1]) / N - gamma * X[1]
    return Y


T_range = np.arange(0,T + 1)

RES = spi.odeint(funcSIS,INI,T_range)

plt.plot(RES[:,0],color = 'darkblue',label = 'Susceptible',marker = '.')
plt.plot(RES[:,1],color = 'red',label = 'Infection',marker = '.')
plt.title('SIS Model')
plt.legend()
plt.xlabel('Day')
plt.ylabel('Number')
plt.show()

模型三：SIR-Model

易感染者–>感染者—time—>康复者（隔离or抗体）—-no–>易感染者

拐点：infected峰值的时间

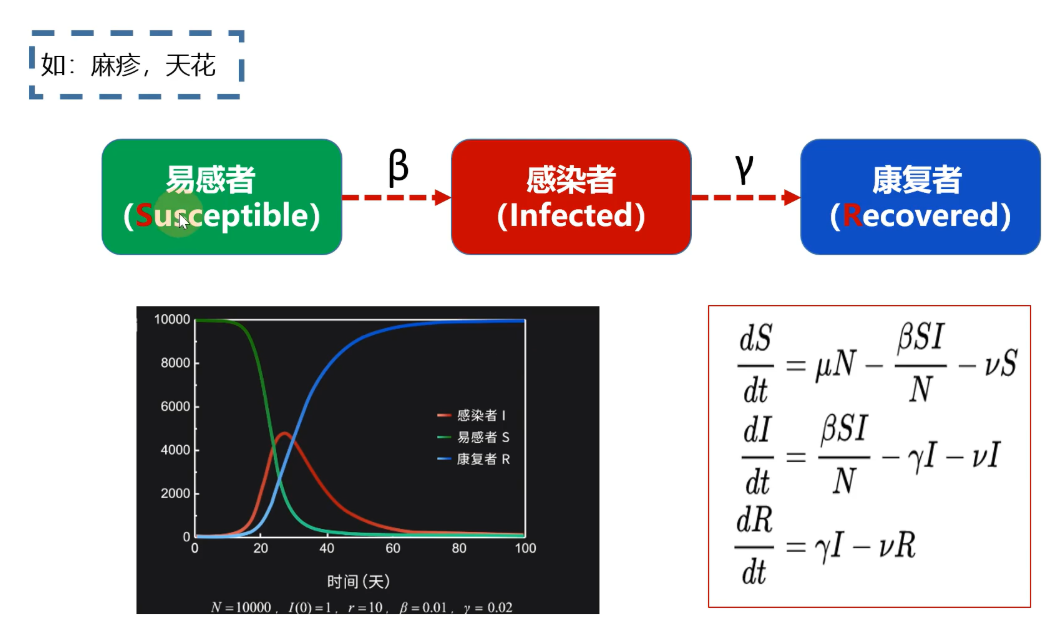
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
import scipy.integrate as spi
import numpy as np
import matplotlib.pyplot as plt

# N为人群总数
N = 10000
# β为传染率系数
beta = 0.25
# gamma为恢复率系数
gamma = 0.05
# I_0为感染者的初始人数
I_0 = 1
# R_0为治愈者的初始人数
R_0 = 0
# S_0为易感者的初始人数
S_0 = N - I_0 - R_0
# T为传播时间
T = 150

# INI为初始状态下的数组
INI = (S_0,I_0,R_0)


def funcSIR(inivalue,_):
    Y = np.zeros(3)
    X = inivalue
    # 易感个体变化
    Y[0] = - (beta * X[0] * X[1]) / N
    # 感染个体变化
    Y[1] = (beta * X[0] * X[1]) / N - gamma * X[1]
    # 治愈个体变化
    Y[2] = gamma * X[1]
    return Y


T_range = np.arange(0,T + 1)

RES = spi.odeint(funcSIR,INI,T_range)

plt.plot(RES[:,0],color = 'darkblue',label = 'Susceptible',marker = '.')
plt.plot(RES[:,1],color = 'red',label = 'Infection',marker = '.')
plt.plot(RES[:,2],color = 'green',label = 'Recovery',marker = '.')
plt.title('SIR Model')
plt.legend()
plt.xlabel('Day')
plt.ylabel('Number')
plt.show()

模型四：SIRS-Model

数学建模常用算法——传染病模型（四）SIRS模型 - 知乎 (zhihu.com)

适用于有易感者、患病者和康复者三类人群，康复者只有暂时性的免疫力，单位时间后变为易感者，有可能再次被感染而患病。

模型假设

易感者与患病者有效接触即被感染，变为患病者，可被治愈再次变为易感者，有短暂免疫力，无潜伏期。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
import scipy.integrate as spi
import numpy as np
import matplotlib.pyplot as plt

# N为人群总数
N = 10000
# β为传染率系数
beta = 0.25
# gamma为恢复率系数
gamma = 0.05
# Ts为抗体持续时间
Ts = 7
# I_0为感染者的初始人数
I_0 = 1
# R_0为治愈者的初始人数
R_0 = 0
# S_0为易感者的初始人数
S_0 = N - I_0 - R_0
# T为传播时间
T = 150

# INI为初始状态下的数组
INI = (S_0,I_0,R_0)


def funcSIRS(inivalue,_):
    Y = np.zeros(3)
    X = inivalue
    # 易感个体变化
    Y[0] = - (beta * X[0] * X[1]) / N + X[2] / Ts
    # 感染个体变化
    Y[1] = (beta * X[0] * X[1]) / N - gamma * X[1]
    # 治愈个体变化
    Y[2] = gamma * X[1] - X[2] / Ts
    return Y


T_range = np.arange(0,T + 1)

RES = spi.odeint(funcSIRS,INI,T_range)

plt.plot(RES[:,0],color = 'darkblue',label = 'Susceptible',marker = '.')
plt.plot(RES[:,1],color = 'red',label = 'Infection',marker = '.')
plt.plot(RES[:,2],color = 'green',label = 'Recovery',marker = '.')
plt.title('SIRS Model')
plt.legend()
plt.xlabel('Day')
plt.ylabel('Number')
plt.show()

模型五：SEIR-Model

暴露者：处于潜伏期的人，有一定概率变成感染者

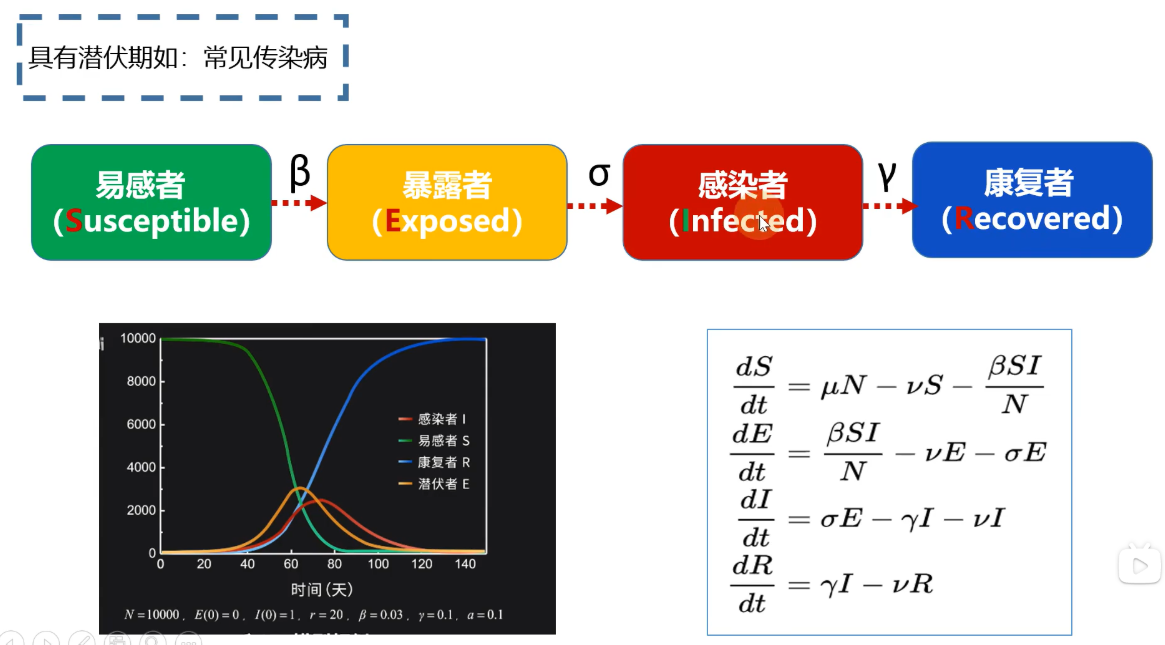
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
import scipy.integrate as spi
import numpy as np
import matplotlib.pyplot as plt

# N为人群总数
N = 10000
# β为传染率系数
beta = 0.6
# gamma为恢复率系数
gamma = 0.1
# Te为疾病潜伏期
Te = 14
# I_0为感染者的初始人数
I_0 = 1
# E_0为潜伏者的初始人数
E_0 = 0
# R_0为治愈者的初始人数
R_0 = 0
# S_0为易感者的初始人数
S_0 = N - I_0 - E_0 - R_0
# T为传播时间
T = 150

# INI为初始状态下的数组
INI = (S_0,E_0,I_0,R_0)


def funcSEIR(inivalue,_):
    Y = np.zeros(4)
    X = inivalue
    # 易感个体变化
    Y[0] = - (beta * X[0] * X[2]) / N
    # 潜伏个体变化
    Y[1] = (beta * X[0] * X[2]) / N - X[1] / Te
    # 感染个体变化
    Y[2] = X[1] / Te - gamma * X[2]
    # 治愈个体变化
    Y[3] = gamma * X[2]
    return Y


T_range = np.arange(0,T + 1)

RES = spi.odeint(funcSEIR,INI,T_range)

plt.plot(RES[:,0],color = 'darkblue',label = 'Susceptible',marker = '.')
plt.plot(RES[:,1],color = 'orange',label = 'Exposed',marker = '.')
plt.plot(RES[:,2],color = 'red',label = 'Infection',marker = '.')
plt.plot(RES[:,3],color = 'green',label = 'Recovery',marker = '.')

plt.title('SEIR Model')
plt.legend()
plt.xlabel('Day')
plt.ylabel('Number')
plt.show()

模型六：SEIRS-Model

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
import scipy.integrate as spi
import numpy as np
import matplotlib.pyplot as plt

# N为人群总数
N = 10000
# β为传染率系数
beta = 0.6
# gamma为恢复率系数
gamma = 0.1
# Ts为抗体持续时间
Ts = 7
# Te为疾病潜伏期
Te = 14
# I_0为感染者的初始人数
I_0 = 1
# E_0为潜伏者的初始人数
E_0 = 0
# R_0为治愈者的初始人数
R_0 = 0
# S_0为易感者的初始人数
S_0 = N - I_0 - E_0 - R_0
# T为传播时间
T = 150

# INI为初始状态下的数组
INI = (S_0,E_0,I_0,R_0)


def funcSEIRS(inivalue,_):
    Y = np.zeros(4)
    X = inivalue
    # 易感个体变化
    Y[0] = - (beta * X[0] * X[2]) / N + X[3] / Ts
    # 潜伏个体变化
    Y[1] = (beta * X[0] * X[2]) / N - X[1] / Te
    # 感染个体变化
    Y[2] = X[1] / Te - gamma * X[2]
    # 治愈个体变化
    Y[3] = gamma * X[2] - X[3] / Ts
    return Y


T_range = np.arange(0,T + 1)

RES = spi.odeint(funcSEIRS,INI,T_range)

plt.plot(RES[:,0],color = 'darkblue',label = 'Susceptible',marker = '.')
plt.plot(RES[:,1],color = 'orange',label = 'Exposed',marker = '.')
plt.plot(RES[:,2],color = 'red',label = 'Infection',marker = '.')
plt.plot(RES[:,3],color = 'green',label = 'Recovery',marker = '.')

plt.title('SEIRS Model')
plt.legend()
plt.xlabel('Day')
plt.ylabel('Number')
plt.show()