2021-05-23

Framework-Thinking

Backtracking Algorithm

算法介绍

实际场景中，解决问题的出发点有多种，为了确认这些出发点是否真的可以解决问题，我们需要逐一测试，找出 1 个甚至所有可行的解决方案，必要时还需要从众多可行方案中找出一个最优的方案。这种情况下，就可以优先考虑回溯算法。

回溯是一种可查找部分甚至全部解决方案的算法，它能够对所有的可行性方案进行测试，一旦判定某个方案无效，则以回溯的方式继续测试其它的方案，直至测试完所有的方案。

回溯可以简单地理解为“回退”或者“原路返回”，我们以一个实例来理解回溯的含义。如下图所示，找出从 A 到 K 的路径：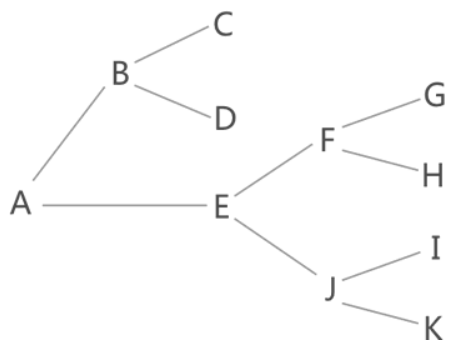

图 1 回溯的含义
显然，从 A 到 K 的路径为 A-E-J-K，但如果要编程实现查找可行的路径，需要一一测试从 A 出发的所有路径，整个查找的过程为：

从 A 出发，有 2 条路径可以选择，先选择 A-B；从 B 出发，又有 2 条路径，先选择 B-C；
到达 C 后，发现无法达到 K，所以放弃此路线，回退至 B，继续测试其他路径（第一次回溯）；
继续探查 B-D，发现也无法到达 K，回退到 B，继续探测其他路径（第二次回溯）；
除 B-C 和 B-D 外，没有其他路径可供选择，回退至 A，探测其他路径（第三次回溯）；
除了 A-B 外，还可以选择 A-E，测试过程同测试 A-B 部分的方式完全相同。

下图给您描绘了测试所有路径所经历的过程：

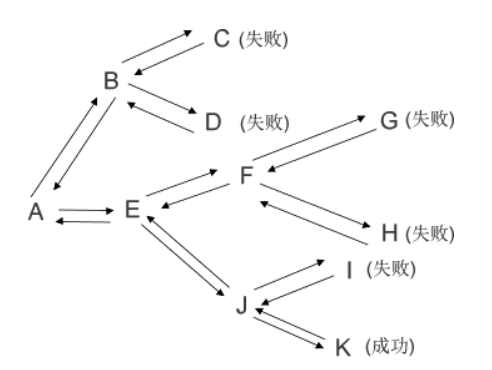
通过不断的回溯，找到解决问题的所有可行方案，这样的算法就称为回溯算法。

算法运用

回溯算法经常以递归的方式实现，该算法常用于解决以下 3 类问题：

决策问题：从众多选择中找到一个可行的解决方案；
优化问题：从众多选择中找到一个最佳的解决方案；
枚举问题：找出能解决问题的所有方案。

经典的适合用回溯算法解决的问题有 N皇后问题、迷宫问题等，我们会在后续章节给大家做详细的讲解。

Divide and conquer algorithm

用空间换时间

算法介绍

实际开发中，我们经常会使用一些巧妙的算法解决问题，分治算法就是其中之一。

分治算法是指采用分而治之的思想，将一个复杂的问题划分成很多相互独立的小问题，通过逐个解决这些小问题，使整个问题得到解决。

使用分治算法解决问题，大致经历 3 个阶段：

分：将整个问题划分为很多相互独立的小问题（子问题），很多小问题还可以进行更细致地划分，直至这些问题不可再分；
治：逐个解决每个子问题，整个过程通常采用递归的方式实现；
合并：合并所有子问题的解决方案，得到整个问题的解决方案。

算法特点

分治算法擅长解决一些规模较大的问题，直接解决此类问题的难度较大，通过将大问题“分而治之”，可以简化问题的难度。此外，由于分解得到的诸多小问题之间是相互独立的，所以可以采用并发执行的方式，提高问题的解决效率。

分治算法的缺陷也很明显，该算法常常采用递归的方式实现，整个过程需要消耗大量的系统资源，严重时还会导致程序崩溃。

算法运用

Greedy Algorithm

计算性价比
根据性价比进行排序（包括weight、value）等
使用while循环控制每次取局部最优解

算法介绍

贪心算法又称贪婪算法，是所有算法中最简单、最易实现的一种算法。

一个问题通常对应有多种算法，每种算法由多个步骤组成。贪心算法解决问题的核心思想是：算法的每一步都选择当前场景中最优的解决方案（又称局部最优解）。

举个例子，假设我们有面值分别为 1、2、5、10 的硬币，要求用尽可能少的硬币拼凑出的总面值为 18。如果采用贪心算法解决此问题，则解决方案为：

选择一个面值为 10 的硬币，可最大程度解决问题，剩余需要拼凑的面值数为 8；
选择一个面值为 5 的硬币，可最大程度解决问题，剩余需要拼凑的面值数为 3；
选择一个面值为 2 的硬币，可最大程度解决问题，剩余需要拼凑的面值数为 1；
选择一个面值为 1 的硬币。

贪心算法每一步都选择的是当前所允许的最大面值的硬币（即局部最优解），整个解决方案也是最优的。

注意，贪心算法并不是在任何场景中都可以得出最优的解决方案。比如，有面值分别为 1、7、10 的硬币，要求用尽可能少的硬币拼凑出的总面值为 15。如果采用贪心算法，则解决方案为：

选择一个面值为 10 的硬币，剩余面值为 5；
选择一个面值为 1 的硬币，剩余面值为 4；
选择一个面值为 1 的硬币，剩余面值为 3；
选择一个面值为 1 的硬币，剩余面值为 2；
选择一个面值为 1 的硬币，剩余面值为 1；
选择一个面值为 1 的硬币。

贪心算法使用了“10+1+1+1+1+1”共 6 枚硬币，但实际上，最优的解决方案只需要“7+7+1”共 3 枚硬币。所以，贪心算法追求的是局部最优解，它并不关心设计的整个解决方案是否最优。

target = 18
price = [1, 2, 5, 10]

price.sort(reverse=True)

i = 0
count = 1
while target > 0:
    if price[i] <= target:
        target -= price[i]
        print('the %d take:%d' % (count, price[i]))
        count += 1
    else:
        i += 1

算法运用

贪心算法可用于解决很多实际问题，例如：

部分背包问题；
使用克鲁斯卡尔算法求最小生成树；
使用迪杰斯特拉算法求两个顶点之间的最短路径。

Dynamic Programming

算法思想

画表，明确dp[i]与dp[i-1]代表的是什么
初始化dp[0]=[0]…
考虑状态转移方程

一般为dp[i] = max/min(dp[i-1], fun(dp[i-1], dp_temp[i]))

即是否考虑此物品的收益

4.完善选此物品和不选此物品的方程即【3】中的方程式

算法介绍

和分治算法类似，动态规划算法也是先将问题分解成多个规模更小、更容易解决的小问题，通过解决这些小问题，从而找到解决整个问题的方法。不同之处在于，分治算法分解的每个小问题都是相互独立的，而动态规划算法分解的小问题之间往往存在关联，比如要想解决问题 A 和问题 B，必须先解决问题 C。

讲解贪心算法时，我们举过一个例子：假设有 3 种面值分别为 1、7 和 10 的硬币，要求用尽可能少的硬币拼凑出的总面值为 15。贪心算法的解决方案为共需要 6 枚硬币（10+1+1+1+1+1），但如果采用动态规划算法，可以找到更优的解决方案，只需要 3 枚硬币（ 7+7+1）。

动态规划算法的解题思路是：用 f(n) 表示凑齐面值为 n 所需要的最少的硬币数量，则面值 15 的拼凑方案有以下 3 种：

f(15) = f(14) +1：选择一枚面值为 1 的硬币，f(14) 表示拼凑出面值 14 所需要的最少的硬币数量；
f(15) = f(8) + 1：选择一枚面值为 7 的硬币，f(8) 表示拼凑出面值 8 所需要的最少的硬币数量；
f(15) = f(5) + 1：选择一枚面值为10 的硬币，f(5) 表示拼凑出面值 5 所需要的最少的硬币数量。

由此，我们将求 f(15) 的值，转换成为了求 min( f(14) , f(8) , f(5) ) 的值（min() 表示取三者中的最小值）。在此基础上，f(14)、f(8)、f(5) 还可以分解为更小的问题：

f(5) = f(4) + 1；
f(8) = f(7) + 1 = f(1) +1；
f(14) = f(13)+1 = f(7) + 1 = f(4) +1。

通过不断地分解，问题的规模会不断地减小，直至分解为 f(0) 或 f(1) 这类很简单的子问题。也就是说，我们只需要求得 f(0) 和f(1) 的值，所有小问题都可以得到解决（如表 1 所示）。

子问题	分解方案	最佳方案	硬币数量
f(0)	不可再分	不选择任何硬币	0
f(1)	f(0) + 1	“1”	1
f(2)	f(1) + 1	“1+1”	2
f(3)	f(2) + 1	“1+1+1”	3
f(4)	f(3) + 1	“1+1+1+1”	4
f(5)	f(4) + 1	“1+1+1+1+1”	5
f(6)	f(5) + 1	“1+1+1+1+1+1”	6
f(7)	f(6) + 1 , f(0) + 1	“7”	1
f(8)	f(7) + 1 , f(1) + 1	“7+1”	2
f(9)	f(8) + 1 , f(2) + 1	“7+1+1”	3
f(10)	f(9) + 1 , f(3) + 1 , f(0) + 1	“10”	1
f(11)	f(10) + 1 , f(4) + 1 , f(1) + 1	“10+1”	2
f(12)	f(11) + 1 , f(5) + 1 , f(2) + 1	“10+1+1”	3
f(13)	f(12) + 1 , f(6) + 1 , f(3) + 1	“10+1+1+1”	4
f(14)	f(13) + 1 , f(7) + 1 , f(4) + 1	“7+7”	2
f(15)	f(14) + 1 , f(8) + 1 , f(5) + 1	“7+7+1”	3

表 1 中借助 f(0) 和 f(1) 的值，依次推导出了 f(2)~f(15) 的值。因此，我们可以很容易得出“拼凑总面值为 15 只需要 7+7+1 共 3 个硬币”的最佳解决方案，这样解决问题的方法就称为动态规划算法。

算法运用

如下给您列举了几个适合采用动态规划算法解决的经典案例：

0-1背包问题；
弗洛伊德算法解决最短路径问题；
最长公共子序列问题；

经典算法题

N皇后问题[回溯+递归]

问题介绍

在国际象棋中，皇后是整个棋盘上实力最强的一种棋子，可以直走、横走和斜着走（沿 45 ° 角移动），可以攻击行走路线上的任何棋子。

N 皇后问题就源自国际象棋，它研究的是：如何将 N 个皇后摆放在 N*N 的棋盘中，使它们不能相互攻击。也就是说，棋盘上各个皇后无论直走、横走还是斜着走，都无法相互攻击。

举个例子，如下在 4*4 的棋盘中摆放了 4 个皇后，它们都用 Q 来表示。

问题思路

显然要想使各个皇后不相互攻击，应保证它们不位于同一行（或者同一列）。借助回溯算法，我们可以逐一测试出每一行皇后所在的位置，最终得出 N 皇后问题的解决方案。

代码实现

count = 0    #统计解决方案的个数
q = [0]*20   #记录各个皇后的放置位置，最终放置 20 个皇后
#输出 N 皇后问题的解决方案
def display(n):
    global count
    count = count + 1
    print("输出第%d个解：" % (count))
    for i in range(1 , n + 1):
        for j in range(1 , n + 1):
            if q[i] != j:
                print("x",end=" ");
            else:
                print("Q",end=" ");
        print()
    print()
#检验第k行的第j列是否可以摆放皇后
def isSafe(k , j):
    for i in range(1 , k):
        #如果有其它皇后位置同一列上，或者位于该位置的斜线位置上，则该位置无法使用
        if q[i] == j or abs(i - k) == abs(q[i] - j):
            return False
    return True
#放置皇后到棋盘上
def n_queens(k , n):
    if k > n:      #递归的出口
        display(n)
    else:
        for j in range(1 , n + 1): #试探第k行的每一列，找到符合要求的列
            if isSafe(k , j):
                q[k] = j
                n_queens(k + 1 , n); #在确认第 k 行皇后位置的前提下，继续测试下一行皇后的位置
print("请输入皇后个数：")
n = int(input());
n_queens(1,n)
print("共有 %d 种不同的排列" % (count))

迷宫问题[回溯+递归]

问题介绍

假设有一个 N*N 的正方形迷宫（如图 1 所示），老鼠必须从起始点移动到终点，它可以向上、向下、向左、向右移动，但仅限于在白色区域内移动。

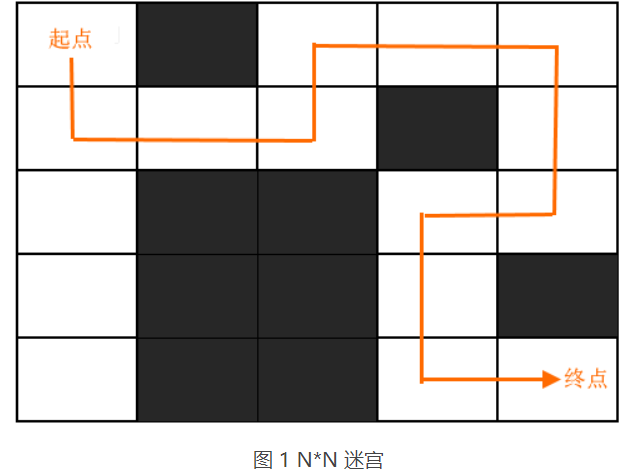
回溯算法可以很好地解决类似的迷宫问题，该算法能够从起点开始，逐一测试所有的移动路线，并最终找到能够达到终点的移动路线。

问题思路

通过使用回溯不断“试错”，直到找出最优路径

假设迷宫中可行走的白色区域用 1 表示，不能行走的黑色区域用 0 表示，图 1 的迷宫可以用如下的矩阵表示：

1 0 1 1 1
1 1 1 0 1
1 0 0 1 1
1 0 0 1 0
1 0 0 1 1

代码实现

# 指定地图的行数和列数
ROW = 5
COL = 5
# 初始化地图
maze = [['1', '0', '1', '1', '1'],
        ['1', '1', '1', '0', '1'],
        ['1', '0', '0', '1', '1'],
        ['1', '0', '0', '1', '0'],
        ['1', '0', '0', '1', '1']]
# 假设当前迷宫中没有起点到终点的路线
find = False


# 回溯算法查找可行路线
def maze_puzzle(maze, row, col, outrow, outcol):
    global find
    maze[row][col] = 'Y'
    if row == outrow and col == outcol:
        find = True
        print("成功走出迷宫,路线图为：")
        printmaze(maze)
    if canMove(maze, row-1, col):
        maze_puzzle(maze, row - 1, col, outrow, outcol)
    # 如果程序不结束，表明此路不通，恢复该区域的标记
        maze[row - 1][col] = '1'
    if canMove(maze, row, col - 1):
        maze_puzzle(maze, row, col - 1, outrow, outcol)
    # 如果程序不结束，表明此路不通，恢复该区域的标记
        maze[row][col - 1] = '1'
    # 尝试向下移动
    if canMove(maze, row + 1, col):
        maze_puzzle(maze, row + 1, col, outrow, outcol)
    # 如果程序不结束，表明此路不通，恢复该区域的标记
        maze[row + 1][col] = '1'
    # 尝试向右移动
    if canMove(maze, row, col + 1):
        maze_puzzle(maze, row, col + 1, outrow, outcol)
    # 如果程序不结束，表明此路不通，恢复该区域的标记
        maze[row][col + 1] = '1'


# 判断指定路线是否可以行走
def canMove(maze, row, col):
    return 0 <= row <= ROW - 1 and 0 <= col <= COL - 1 and maze[row][col] != '0' and maze[row][col] != 'Y'


# 输出行走路线
def printmaze(maze):
    for i in range(0, ROW):
        for j in range(0, COL):
            print(maze[i][j], end=" ")
        print(end='\n')


maze_puzzle(maze, 0, 0, ROW-1, COL-1)
if find is False:
    print("未找到可行路线")

部分背包问题[贪婪算法]

问题介绍

背包问题指的是在背包所能承受的重量范围内，将哪些物品装入背包可以获得最大的收益？

举个例子，一个小偷正在商店行窃，他随身携带的背包可以装一定重量的商品，商店中摆放着不同重量和价值的商品，小偷应该如何选择才能获得最大的收益？这样的问题就属于背包问题。

根据所选物品是否可再分（比如选择某物品的 1/2），背包问题可分为以下两种：

0-1 背包问题：挑选物品时，单个物品要么放弃，要么全部装入背包，不存在“装入 1/2 物品”的情况；
部分背包问题：挑选物品时，单个物品可再分，例如将物品的 1/2 装入背包。

本节给您讲解的是如何使用贪心算法解决部分背包问题。

问题思路

接下来以“小偷在商店行窃，商店的商品都可再分”为例，给您讲解如何解决部分背包问题。

为了方便讲解，我们做以下假设：

背包最多可以承受的商品重量为 W（后续简称承重）；
商店共有 n 件商品，它们都是可再分的，其中第 i 件商品的总重量为 Wi，总收益为 Pi。

显然，要想获得最大的收益，小偷需要做到以下 2 点：

充分利用背包的承重，背包装的商品越多，获得收益就越大；
确保选中的 W 重量商品中，单位重量下获得的收益最大。

结合以上 2 点，我们可以采用贪心算法来解决这个问题，具体的解决方案是：计算每个商品的收益率（即 Pi/Wi），优先选择收益率最大的商品，直至选择的商品总重量恰好为 W。

假设背包的承重为 20，商店中共有 3 种商品，它们的重量和收益分别为：

商品 1：重量 10，收益 60，单位重量的收益为 6；
商品 2：重量 20，收益 100，单位重量的收益为 5；
商品 3：重量 30，收益 120，单位重量的收益为 4。

通过比较收益率，以上 3 种商品装入背包的顺序依次为：商品 1 > 商品 2 > 商品 3。受到背包承重的限制，商品 1 可以全部装入背包，而商品 2 只能装一半（10 斤），商品 3 无法被装入。

代码实现

W = 50
w = [10, 30, 20]
p = [60, 100, 120]
value = 0
result = [0] * len(w)

v = []
for i in range(len(w)):
    v.append(p[i]/w[i])

for j in range(len(w)):
    for i in range(j+1, len(w)):
        if v[j] < v[i]:
            v[j], v[i] = v[i], v[j]
            w[j], w[i] = w[i], w[j]
            p[j], p[i] = p[i], p[j]

i = 0
while W > 0:
    temp = min(W, w[i])
    result[i] = temp / w[i]
    i += 1
    W -= temp

for i in range(len(result)):
    if result[i] == 1:
        print('weight:%f, total value:%f-->100%%' % (w[i], p[i]))
        value += p[i]
    elif result[i] == 0:
        print('weight:%f, total value:%f-->0%%' % (w[i], p[i]))
    else:
        print('weight:%f, total value:%f-->%f' % (w[i], p[i], result[i]*100))
        value += p[i]*result[i]

print('the total value:%f' % value)

01背包问题[动态规划]

问题介绍

仍以小偷在商店行窃为例，他随身携带的背包可以装一定重量的商品，商店中摆放着不同重量和价值的商品，小偷如何选择能获得最大的收益？在 01背包问题中，每种商品都是不可再分的，小偷在选择商品时，要么装入整个商品，要么放弃装该商品，不存在“装某商品的 1/2”的情况。

贪心算法仅适用于解决部分背包问题，不再适合解决 01背包问题。举个例子，假设商店摆放着以下几种商品：

商品 1 ：重量为 6，收益为 6；
商品 2 ：重量为 2，收益为 4；
商品 3 ：重量为 3，收益为 4；
商品 4 ：重量为 5，收益为 3。

假设背包可容纳商品的最大重量为 7，如果采用贪心算法，首先会选取收益最大的商品 1，此时背包的剩余承重为 1，无法再装下其他商品，因此最终获得的收益为 6。实际上还有一种更好的解决方案，即选择装入商品 2 和商品 3，总重量为 5（<7），总收益为 4 + 4 = 8。

显然，贪心算法不再适用于解决 01背包问题，解决此问题可以使用动态规划算法。

问题思路

假设背包可以承受的最大重量为 11，商店有 5 种商品，它们的重量和价值分别为：

wi 表示第 i 种商品的重量，vi 表示第 i 种商品的价值
w1 = 1，v1 = 1
w2 = 2，v2 = 6
w3 = 5，v3 = 18
w4 = 6，v4 = 22
w5 = 7，v5 = 28

采用动态规划算法解决此问题的具体过程是：

从背包所能承受的最大重量为 1 开始，依次推导出各个承重条件下所能获得的最大收益。

建立如下这张表格，逐一分析出各个载重量下每一个商品装与不装对收益值的影响，从而获得各个载重量对应的最大收益值。

背包载重量	0	1	2	3	4	5	6	7	8	9	10	11
w1 = 1，v1 = 1	0
w2 = 2，v2 = 6	0
w3 = 5，v3 = 18	0
w4 = 6，v4 = 22	0
w5 = 7，v5 = 28	0

当背包载重量为 0 时，无法装入各个商品，因此收益一直为 0。

首先考虑商品 (w1 , v1)，当背包载重量分别为 1、2、…、11 时，都可以装入此商品，且和不装该商品相比（背包是空的），装该商品的收益更大，因此对上表进行更新：

背包载重量	1	2	3	4	5	6	7	8	9	10	11
w1 = 1，v1 = 1	1	1	1	1	1	1	1	1	1	1	1
w2 = 2，v2 = 6
w3 = 5，v3 = 18
w4 = 6，v4 = 22
w5 = 7，v5 = 28

再分析商品 (w2，v2)：

载重量为 1 时：w2>1，无法装入该商品，最大收益仍为 1。
载重量为 2 时：背包可以装入此商品，装入此商品对应的总收益可以用 6+f(0) 表示，其中 f(0) 指的是载重量为 0 时装 (w1,v1) 对应的最佳收益。从上表可知，f(0) = 0，因此 6+f(0)=6，比先前只装 (w1 , v1) 的收益大。
载重量为 3 时：背包可以装入此商品，装入此商品对应的总收益可以用 6+f(1) 表示，f(1) 指的是载重量为 1 时装 (w1 , v1) 对应的最佳收益。从上表可知，f(1) = 1，因此 6+f(1) = 7，比先前只装 (w1 , v1) 的收益大。
载重量为 4~11：背包可以装入此商品，且装此商品的收益总比不装时的大，总收益都为 7。

继续对表格进行更新：

背包载重量	1	2	3	4	5	6	7	8	9	10	11
w1 = 1，v1 = 1	1	1	1	1	1	1	1	1	1	1	1
w2 = 2，v2 = 6	1	6	7	7	7	7	7	7	7	7	7
w3 = 5，v3 = 18
w4 = 6，v4 = 22
w5 = 7，v5 = 28

再分析商品 (w3 , v3)：

载重量为 1 时：w3>1，无法装入该商品，最大收益仍为 1。
载重量为 2 时：w3>1，无法装入该商品，最大收益仍为 6。
载重量为 3~4 时：w3>1，无法装入该商品，最大收益仍为 7。
载重量为 5：背包可以装入此商品，且装此商品的总收益可以用 18+f(0) 表示，f(0) 指的是载重量为 0 时装 (w2 , v2) 对应的最佳收益。从上表可知，f(0) = 0，因此 18+f(0) = 18，比先前统计的收益值更高。
载重量为 6：背包可以装入此商品，且装此商品的总收益可以用 18+f(1) 表示，f(1) 指的是载重量为 1 时装 (w2 , v2) 对应的最佳收益。从上表可知，f(1) = 1，因此 18+f(1) = 19，比先前统计的收益值更高。
载重量为 7：背包可以装入此商品，且装此商品的总收益可以用 18+f(2) 表示，f(2) 指的是载重量为 2 时装 (w2 , v2) 对应的最佳收益。从上表可知，f(2) = 6，因此 18+f(2) = 24，比先前统计的收益值更高。
根据此规律可以依次求得载重量分别为 8、9、…、11 时，对应的总收益为 25。

继续对表格进行更新：

背包载重量	1	2	3	4	5	6	7	8	9	10	11
w1 = 1，v1 = 1	1	1	1	1	1	1	1	1	1	1	1
w2 = 2，v2 = 6	1	6	7	7	7	7	7	7	7	7	7
w3 = 5，v3 = 18	1	6	7	7	18	19	24	25	25	25	25
w4 = 6，v4 = 22
w5 = 7，v5 = 28

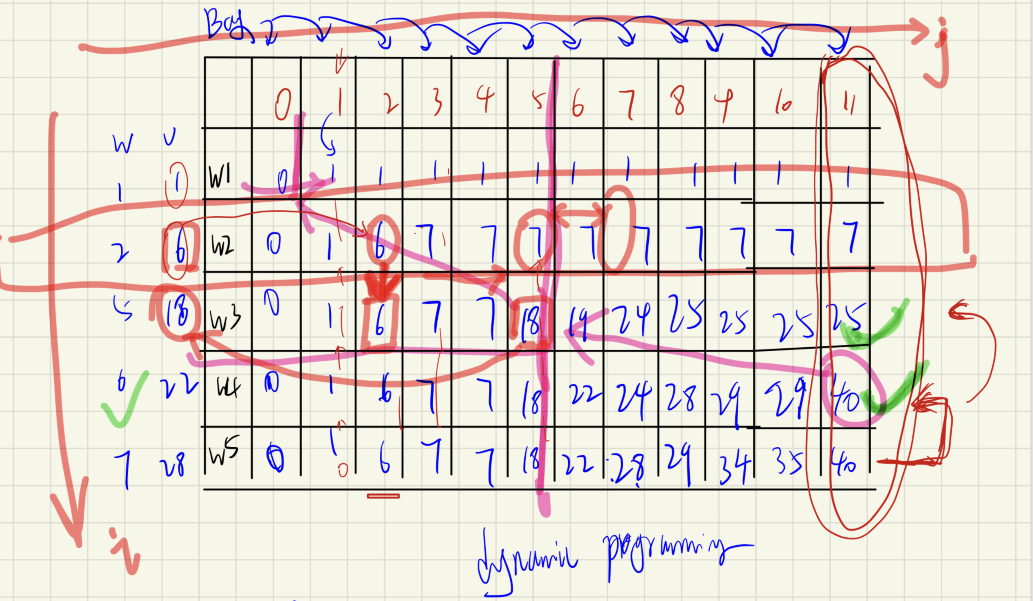
借助 (w3 , v3) 的收益数据，我们可以继续推导出不同载重量对应的 (w4 , v4) 商品的收益值；同理借助 (w4 , v4) 的收益数据，可以推导出不同载重量对应的 (w5 , v5) 商品的收益值。推导结果如下所示：

背包载重量	1	2	3	4	5	6	7	8	9	10	11
w1 = 1，v1 = 1	1	1	1	1	1	1	1	1	1	1	1
w2 = 2，v2 = 6	1	6	7	7	7	7	7	7	7	7	7
w3 = 5，v3 = 18	1	6	7	7	18	19	24	25	25	25	25
w4 = 6，v4 = 22	1	6	7	7	18	22	24	28	29	29	40
w5 = 7，v5 = 28	1	6	7	7	18	22	28	29	34	35	40

因此借助动态规划算法，当背包的载重量为 11 时，获得的最大收益为 40。

代码实现

N = 5       # 设定商品的种类
W = 11      # 设定背包的最大载重量
w = [0, 1, 2, 5, 6, 7]    # 商品的载重，不使用 w[0]
v = [0, 1, 6, 18, 22, 28]   # 商品的价值，不使用 v[0]
# 二维列表，记录统计数据
result = [[0]*(W+1) for _ in range(len(w))]
# 动态规划算法解决01背包问题

# 逐个遍历每个商品
for i in range(1, N+1):
    # 求出从 1 到 W 各个载重对应的最大收益
    for j in range(1, W+1):
        # 如果背包载重小于商品总重量，则该商品无法放入背包，收益不变
        if j < w[i]:
            result[i][j] = result[i-1][j]
        else:
            # 比较装入该商品和不装该商品，哪种情况获得的收益更大，记录最大收益值
            result[i][j] = max(result[i-1][j], v[i]+result[i-1][j-w[i]])
print(result)
print("背包可容纳重量为 %d,最大收益为 %d" % (W, result[N][W]))

# 追溯选中的商品
n = N
bagw = W
# 逐个商品进行判断
print("所选商品为:")
while n > 0:
    # 如果在指定载重量下，该商品对应的收益和上一个商品对应的收益相同，则表明未选中
    if result[n][bagw] == result[n-1][bagw]:
        n = n - 1
    else:
        # 输出被选用商品的重量和价值
        print("(%d,%d) " % (w[n], v[n]))
        # 删除被选用商品的载重量，以便继续遍历
        bagw = bagw - w[n]
        n = n - 1

简化后的code

N = 5
W = 11
w = [0, 1, 2, 5, 6, 7]
v = [0, 1, 6, 18, 22, 28]

result = [[0]*(W+1) for _ in range(N+1)]

for i in range(1, N+1):
    for j in range(1, W+1):
        if j < w[i]:
            result[i][j] = result[i-1][j]
        else:
            result[i][j] = max(result[i-1][j], v[i]+result[i-1][j-w[i]])

print('bag`s weight:%d, total value:%d' % (W, result[N][W]))

print('The selected products are:')
n = N
bagw = W
while n > 0:
    if result[n][bagw] == result[n-1][bagw]:
        n -= 1
    else:
        print('({}, {})'.format(w[n], v[n]))
        bagw -= w[n]
        n -= 1

List

一般情况下使用index进行列表的切分比使用[:]–>[start:end)的时间复杂度更低，效率也更高O(1）<–>O（n）
对于具有特殊意义的index一般追踪起来比较困难，我们选择直接再terminal中return对应的information而不是return index

Drink`s Blog

Framework-Thinking

Backtracking Algorithm

算法介绍

算法运用

Divide and conquer algorithm

算法介绍

算法特点

算法运用

Greedy Algorithm

算法介绍

算法运用

Dynamic Programming

算法思想

算法介绍

算法运用

N皇后问题[回溯+递归]

问题介绍

问题思路

代码实现

迷宫问题[回溯+递归]

问题介绍

问题思路

代码实现

部分背包问题[贪婪算法]

问题介绍

问题思路

代码实现

01背包问题[动态规划]

问题介绍

问题思路

代码实现

List

String

Set

Dictionary

Tuple

Linked List